Bangun ruang kubus – Setelah sebelumnya membahas tentang rumus segitiga, kali ini kami akan membahas mengenai rumus bangun ruang kubus. hal-hal yang akan dibahas adalah pengertian, sifat-sifat kubus serta tentang rumus kubus dari rumus volume, luas, dan keliling kubus.
Untuk melihat daftar isinya, kamu bisa lihat di bawah ini.
Bangun Ruang Kubus
A. Pengertian
Bangun ruang kubus merupakan bangun ruang yang memiliki bentuk tiga dimensi yang telah dibatasi oleh 6 bidang sisinya dan sisi tersebut berbentuk kongruen atau berbentuk bujur sangkar. Kubus memiliki rusuk yang sama panjangnya yang berjumlah 12 rusuk.
Kemudian bangun ruang kubus bisa juga disebut dengan bidang enam beraturan yang berbentuk mirip dengan prisma segi empat.
B. Ciri-Ciri
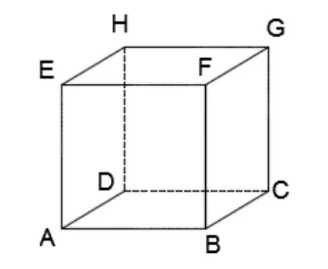
Berikut ini merupakan ciri-ciri bangun ruang kubus:
- Jumlah bidang sisi ada 6 buah yang berbentuk bujur sangkar yaitu ABCD.
- Kubus mempunyai 8 buah titik sudut yakni A, B, C, D, E, F, G, H.
- Memiliki 12 buah rusuk yang sama panjangnya yaitu AB, CD, EF, GH, AE, BF, CG, DH, AD, BC, EH, FG.
- Mempunyai sudut yang semuanya siku-siku.
- Mempunyai 4 diagonal ruang dan 12 diagonal bidang. Diagonal ruang pada gambar diatas yaitu garis AG, BH, CE, DF sedangkan diagonal bidangnya yaitu garis AC BD, EG, FH, DE, AH, CF, BG, AF, BE, DG, dan CH.
C. Gambar Jaring-Jaring
Jaring jaring adalah bidang datar yang berupa gabungan dari bangun datar yang menyusun sebuah bangun ruang seperti balok, kubus, limas, dan lainnya.
Jaring jaring dapat diperoleh dengan cara membelah sebuah bangun ruang dengan mengikuti rusuk-rusuknya. Jaring-jaring kubus terdiri dari 6 buah bangun datar persegi atau bujur sangkar.
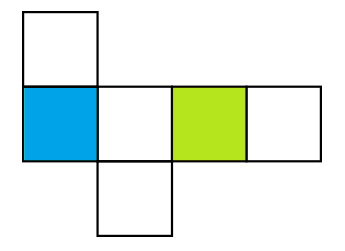
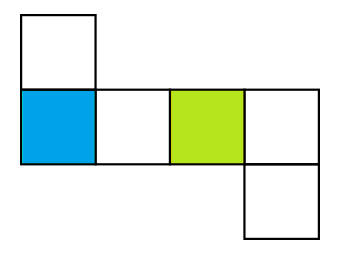
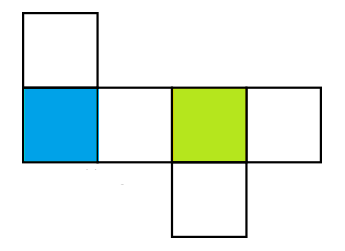
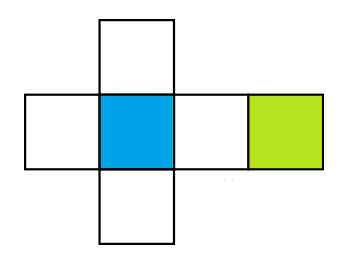
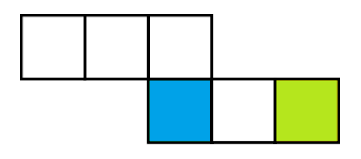
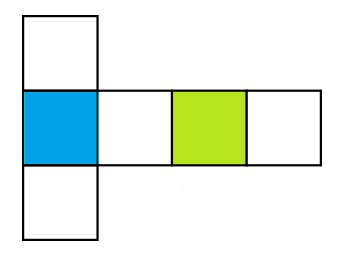
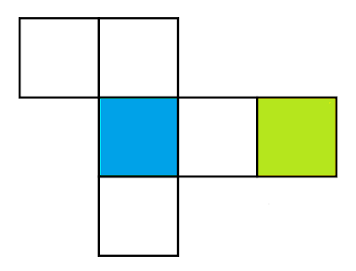
Berikut merupakan gambar jaring-jaring kubus.
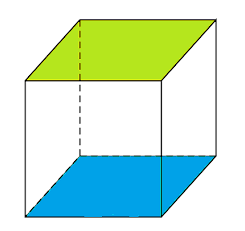
Gambar diatas adalah gambar sebuah kubus yang akan kita cari jaring-jaringnya, warna biru adalah alasnya, dan warna hijau adalah tutupnya.
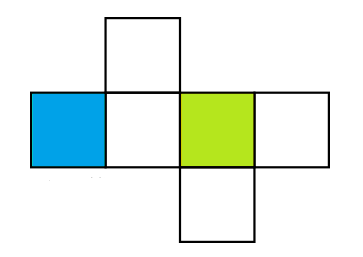

Baca Juga Bangun Ruang Balok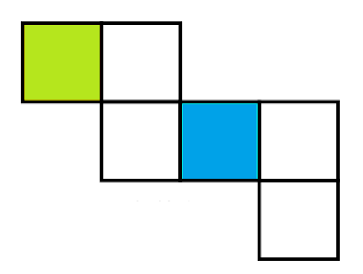
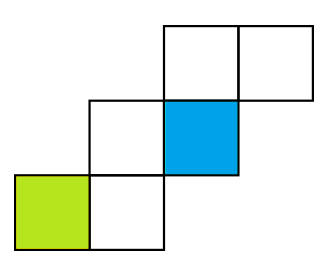
E. Tabel Rumus Kubus
| Perhitungan | Rumus | Satuan |
| Rumus Volume Kubus | V = s x s x s V = s3 | m3 |
| Rumus Luas Permukaan Kubus | L = 6 x s2 | m2 |
| Rumus Keliling Kubus | K = 12 x s | m |
| Rumus 1 Diagonal Sisi Kubus | Ds = s√2 | m |
| Rumus Diagonal Sisi Kubus | Ds = 12 x s√2 | m |
| Rumus 1 Diagonal Ruang Kubus | Dr = s√3 | m |
| Rumus Diagonal Ruang Kubus | Dr = 4 x s√3 | m |
| Luas 1 Bidang Diagonal Kubus | L = s²√2 | m2 |
| Luas Bidang Diagonal Kubus | L = 6 x s²√2 | m2 |
Keterangan:
V = Volume
L = Luas
K = Keliling
Ds = Diagonal Sisi
Dr = Diagonal Ruang
r = sisi
m3 = Meter Kubik
m2 = Meter Persegi
m = Meter
Catatan: Untuk satuan hanya menjelaskan pangkatnya saja, tidak selalu m (meter). Bisa juga jadi cm3, dm3, dan lainnya.
Baca Juga
F. Rumus Kubus
1. Cara Menghitung Rumus Volume Kubus
Menghitung rumus volume kubus diperlukan isi dari kubus itu sendiri, besarnya volume merupakan perpaduan antara perkalian dari sisi panjang, lebar dan tinggi. Sedangkan untuk ukuran rusuk dari sebuah bangun ruang kubus itu semuanya sama yaitu r. maka rumus volume kubus dapat dinyatakan seperti dibawah ini.
Volume Kubus (V) = s x s x s atau V = s³
2. Cara Menghitung Rumus Luas Kubus Rumus
Menghitung luas kubus diperlukan jumlah dari luas permukaan kubus tersebut dan permukaan bangun ruang kubus memiliki 6. Untuk itu rumus bisa dinyatakan seperti rumus matematika dibawah ini.
Luas Permukaan Kubus (L) = 6 x s²
3. Cara Menghitung Rumus Keliling Kubus
Menghitung keliling kubus diperlukan panjang dari rusuk suatu kubus. kubus memiliki rusuk sebanyak 12 rusuk. Untuk itu rumus keliling kubus bisa dinyatakan seperti rumus matematika dibawah ini.
Keliling Kubus (K) = 12 x s
Baca Juga Bangun Datar TrapesiumContoh Soal
Contoh Soal 1:
Diketahui sebuah bangun ruang kubus dengan panjang sisi sebuah kubus sebesar 10 cm, maka hitunglah volume, luas permukaan, dan keliling kubus tersebut.
Penyelesaian:
Diketahui:
s = 10 cm
Ditanya:
V = …? L = …? K = …?
Jawab:
Rumus Volume Kubus: V = s³
V = 10³ = 1000 cm³
Rumus Luas Permukaan Kubus: L = 6 x s²
L = 6 x 10²
L = 6 x 100 = 600 cm²
Rumus Keliling Kubus: K = 12 x s
K = 12 x 10 = 120 cm
Jadi, volumenya adalah 1000 cm³, luas permukaannya 600 cm², dan keliling kubus adalah 120 cm.
Contoh Soal 2:
Lemari baju budi berbentuk kubus memiliki panjang, lebar, dan sisi yang sama yaitu 3 meter, Hitunglah volume dari lemari baju budi tersebut.
Penyelesaian:
Diketahui: s = 3 meter
Ditanya: V= …?
Jawab:
V = s x s x s
V = 3 x 3 x 3 = 27 m³
Contoh Soal 3:
Ada Sebuah kayu berbentuk kubus yang memiliki panjang sisi yaitu 5 cm. Cari dan hitunglah keliling kayu berbentuk kubus tersebut.
Penyelesaian:
Diketahui: s = 5 cm
Ditanya: K = …?
Jawab:
K = 12 x s
K = 12 x 3
K = 36 cm
Jadi, keliling kayu berbentuk kubus tersebut adalah 36 cm.
Contoh Soal 4:
Ada sebuah papan berbentuk kubus yang memiliki panjang sisi yaitu 10 cm. Cari dan hitunglah keliling papan yang berbentuk kubus tersebut.
Penyelesaian:
Diketahui: s = 10 cm
Ditanya: K = …?
Jawab:
K = 12 x s
K = 12 x 10
K = 120 cm
Jadi, keliling papan berbentuk kubus tersebut adalah 120 cm
Inilah pembahasan lengkap mengenai bangun ruang kubus, dari mulai ciri-ciri sampai rumus kubus. Semoga dapat menambah ilmunya, dan jangan lupa untuk membaca artikel lainnya. Terima kasih!!
